Resolución de la conjetura de Goldbach, por MJP

¡¿Cuán inteligente eres?! - How smart are you?!

Spanish:
Todas las obras publicadas en este blog, son Obras Inéditas, y cuento con el Registro Nacional de la Propiedad Intelectual de cada una de ellas, por lo que quedan:

Reservados todos los derechos. De conformidad con lo dispuesto en el artículo 270 del Código Penal vigente, podrán ser castigados con penas de multa y privación de la libertad quienes reprodujesen o plagiaren en todo o en parte, una obra literaria, artística o científica fijada en cualquier tipo de soporte, sin la preceptiva autorización.
English:

All works published on this Blog are Unpublished Works, and I count on the National Register of Intellectual Property of each: All rights reserved. In accordance with Article 270 of the Penal Code, may be punished by fine and imprisonment those who reproduce or plagiaren in whole or in part, a literary, artistic or scientific fixed in any medium, without the required authorization.

               Resolución de la conjetura de Goldbach por MJP

Resolución de la conjetura de Goldbach, por MJP

A sabiendas de que para que exista una construcción primeramente se deben de asentar sus bases, he decidido entonces comenzar por una de ellas, la cual nace inicialmente como una conjetura para luego develar, que el enunciado propuesta por la misma es verdadero, la misma lleva por nombre:

Conjetura de MJP

De acuerdo con la conjetura de Goldbach, puedo conjeturar que:

Existe al menos un número primo p entre y p₁  y otro número primo p entre p₁  y el duplo de p₁ , es decir entre p₁  y 2p₁ , tal que p₁   sea un número entero cualesquiera y 2 p₁  un número par, siempre y cuando 2 p₁  cumpla la condición de ser equivalente a c, en la conjetura de Goldbach.

Según esta conformación debe de existir un número primo p mayor que p₁  y  2 p₁ . Un ejemplo censillo de esta conjetura, se demuestra de la siguiente forma: Al tomar por ejemplo un primo p para llegar al resultado de que a + b = 34, (un medio) de 34, ½ de 34 es solo para facilitar la deducción de un supuesto.

Entonces 34 = 17 + 17, es decir que, si el número diecisiete, sería

El máximo número primo encontrado hasta 34 + 2, no habría solución para tal resultado y la conjetura de Goldbach sería falsa. Es por ello, que he utilizado el supuesto, para demostrar, no solo que esta conjetura es verdadera sino que además la conjetura de Goldbach, también lo es, la demostración analítica la expondré más adelante, ahora pasaré a explicar lo que es un supuesto en matemática.

Supuesto de MJP: un supuesto, es una posibilidad que nos permite llegar a una solución o no, de un enunciado, a través de una razón lógica, que es axiomática y deducida por medio del análisis matemático.

Añadiré ahora una conjetura, que se halla fuera de la necesidad de análisis para llegar a la resolución de la conjetura de Goldbach, pero como a nacido a partir del estudio de la misma, es que le he dado lugar dentro extensión de este trabajo, la Conjetura lleva por nombre entonces:

Conjetura de los números primos Tfy de MJP:

Los números primos Tfy de MJP, son aquellos que al cambiarles el orden del primer al último digito de los mismos, (números primos Tfy de MJP de cifras que pueden ser leídas de izquierda a derecha y de derecha a izquierda) siguen siendo números primos.

Téngase en cuenta que este enunciado es válido tanto para los números positivos como para los números negativos. A modo de ejemplo, ya que los números primo Tfy de MJP son infinitos, citaré algunos de los números primos Tfy de MJP, que se hallan del uno al cien.

(13, 31), (17, 71), (37, 73), ………,∞

Importante: siempre que trabajemos en las fórmulas, de la resolución de la Conjetura de Goldbach de MJP, con las fórmulas n / ln_{n   ,}hemos de utilizar, solo el valor de la característica y no el de la mantisa, a no ser que ésta, así lo requiera, (como se verá más adelante).

Ahora bien, el enunciado de la conjetura de Goldbach, nos dice que: 

a + b = c {a Λ b Є S p  Λ a Λ b ≥ 3 / c = S _{c par} }

Se lee:

a + b = c tal que a y b pertenecen al conjunto de números primos, y a y b son mayor o igual que 3, tal que es igual, al conjunto de la consecutividad par.

Demostraré ahora el método de la resolución de la conjetura de Goldbach, para determinar si el enunciado propuesto por tal conjetura es verdadero o falso. Ya es sabido de que no existe al menos hasta hoy un patrón entre los números primos. He desarrollado entonces una estructura que es válida solo para los grandes números, la cual, no solo nos permite demostrar que la conjetura de Goldbach, es verdadera, sino que también nos permite calcular cuantas combinaciones entre números primos combinaciones entre números no primos, y combinaciones entre números primos y números no primos, existen en la estructura para cada diagonal de la misma, cálculos que se verán más adelante, a través de continuas deducciones que nacen a partir de la lógica en un extenso y detallado análisis.

A continuación representaré gráficamente, y detallaré teóricamente la estructura, para luego comenzar con el análisis. Téngase en cuenta que esta estructura tiende al infinito, es por ello que la representación grafica es solo a modo de ejemplo, para hacer más inteligible su extensión, en lo referente a su razonamiento analítico.

Expondré ahora la estructura que lleva por nombre:

 Estructura de Números Ascendentes Dependientes de Impares Adicionados de MJP, o bien Estructura  NADIA, de MJP.

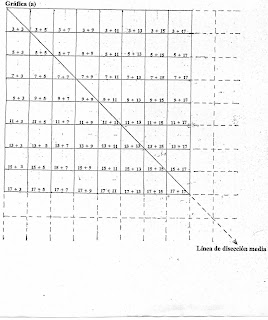
Ejemplo de la estructura NADIA de MJP. (ver en el anexo, gráfica (a))  

La generalización de la Estructura NADIA de MJP, sería entonces:

(ver en el anexo gráfica (b))

Se puede observar que la Estructura NADIA de MJP, esta constituida por patrones modulares, de módulo 3. (ver en anexo gráfica (c)) 

En donde cada patrón tripartito, es decir, cada celda consta de tres partes modulares, además cada patrón, esta dado por la constante 3² , es decir, que la cantidad de patrones que ocupan las tres primeras filas como las tres primeras columnas, esta dada, por la fórmula:

Si:

[(k – 4)/ 2] = C_{C(a, b)}

Se lee:

C_{C(a, b)} : Cantidad de combinaciones con (a, b)

[[(k – 4)/ 2] / 3] = C_{pat..(a, b)}

Se lee:

C_{pat..(a, b)}  : Cantidad de patrones con (a, b)

Se deduce de la fórmula [(k – 4)/ 2] / 3], que los valores de las filas, como de las columnas, son a razón de un tercio de 1/3 por cada patrón, además se observa, que a partir de  [(k – 4)/ 2], que la parte entera de  [(k – 4)/ 2] / 3], multiplicado por si mismo, es decir, elevado al cuadrado nos da, el total de patrones modulares según la fórmula:

[[(k – 4)/ 2] / 3]²  = [ C_{pat..(a, b)} ] ²

Se lee:

[ C_{pat..(a, b)} ] ²: cantidad de patrones en el cuadrado dado por (a, b) 

(Ver en el anexo, gráfica (d))

Puede observarse en las diagonales medias, que los valores del módulo dependen de los resultados, es decir, según sea el valor de K, serán los valores de los módulos tripartitos, que se extienden por toda la diagonal.

Se ha visto así, como la Estructura NADIA de MJP, contiene patrones modulares, y si bien es cierto que podría seguir explayándome en el análisis cuantitativo, de los patrones de modulación tres, será innecesario, debido a que la estructura modular no es la que utilizaré para llegar a la resolución de la conjetura de Goldbach.

Se sabe que n/ln_n nos da la cantidad de números primos que se hallan en un cierto número, se puede observar entonces, en la estructura NADIA de MJP, que a través del análisis, se pueden obtener los porcentajes de los números primos contenidos en [(k – 4)/ 2] ² 

Si:

n/ln = Cp

Se lee:

Cp: Cantidad de números primos

Se entiende entonces que el porcentaje de la cantidad de números primos en el cuadrado de [(k – 4)/ 2] ²  es igual a:

Si:

n/ln_n = Cp

→ k/ln_k = Cp _k

Se lee:

Cp_k: Cantidad de números primos en k

Tal que:

[(k – 4)/ 2]²  = C_{C(a, b)}: Cantidad de combinaciones con (a, b)

Se lee:

C_{C(a, b)}: cantidad de combinaciones en el cuadrado con (a, b)

En consecuencia, si [(k – 4)/ 2]² ; se entiende es la cantidad de combinaciones en el cuadrado. Se razona entonces que la cantidad de números primos combinados entre si en el cuadrado es de  (k/ln_k) ² y que el porcentaje de esa cantidad de combinaciones es:  

Es igual aC_{C(a, b)}:

[(k /ln_k)/ 2] ²  *100%]/ [(k – 4)/ 2]²  = %C_{p(a, b)}

Se lee:

% C_{p (a, b)}: porcentaje de la cantidad de combinaciones primas en el cuadrado con (a, b)

Se deduce entonces que el porcentaje de la cantidad de combinaciones de números no primos en el cuadrado es:

Si:

[(k-4)/ 2] – (k/ln_k) = C _{~ p (a, b)}

Se lee:

C _{~  p (a, b)}: Cantidad de números no primos con (a, b)

Entonces:

(C  _{~  p (a, b)} ) ²= C  _{~  p (a, b)}

Se lee:

C   _{~ p (a, b)}: Cantidad de combinaciones de números no primos con (a, b)

Demás esta decir; que obviamente se pueden obtener otros porcentajes a través del análisis, obteniendo las cantidades de números primos y que los valores de estos porcentajes como otros, se obtienen, por medio de la operación llamada Regla de tres simple, pero como no me son de utilidad para la resolución de este trabajo, lo dejaré de lado, para proseguir con lo siguiente:

Al observar detalladamente la Estructura NADIA de MJP, logré percatarme de que esta estructura, es una estructura de giro, es decir, si lo girare, los valores de k que anteriormente se hallaban sobre una diagonal, ahora se hallan sobre una diagonal en la estructura, ahora se hallan sobre una vertical en la estructura, estructura que le he dado el nombre de: Estructura de Giro de MJP, o bien Estructura G de MJP.

La estructura es la siguiente:

Estructura G de MJP. (Ver en el anexo, gráfica (e))

La fórmula de incremento, del total de combinaciones en la suma de las diagonales, dependen de la fórmula del factorial de 10.

“Téngase en cuenta de ahora en más, que las fórmulas (g. Nª),

corresponden a las gráficas que se hallan en el anexo, (véase al final del trabajo)”.

Es decir:

Si:

Ʃ = (a(a + 1)/ 2)     

(g. 1)  → a = [(k – 4)/ 2]

/ (a + 1) = [ ((k – 4)/ 2) + 1]

(g. 2) Ʃ = [[[(k – 4)/ 2] [ ((k – 4)/ 2) + 1]]/ 2] = T _{c v (a, b)}

Se lee:

T _{c v (a, b)}: total de combinaciones en las diagonales con (a, b)

Queda así definida la Estructura G de MJP, con evidentes razones de semejanza con la Estructura NADIA de MJP, ya que tan solo se diferencian entre ambas, en sus formas, y no así, en su análisis matemático. Es por ello, que sería en vano seguir exponiendo el desarrollo de la estructura en toda su extensión, en lo referente a su análisis matemático.

Se denota entonces, a partir de lo expuesto que en la Estructura NADIA de MJP. Existe una diferencia constante de valor 1;

/ = [ ((k + 2) – 4)/ 2] ; [ ((k  +  2) - k) ] = 2

[ [ ((k + 2) – 4)/ 2] - [ ((k  -  4)/ 2 ] ] = 1 = C  _dif.

Se lee:

C  _dif. : Constante diferencial

C  _dif. = 1

Observación:

Se entiende que si  k /ln_k es igual a la cantidad de números primos hasta k, pues la cantidad de combinaciones entre números primos sobre la línea de disección media, es una axioma determinada por la misma fórmula, es decir, la cantidad de números primos hasta K, es igual a la cantidad de combinaciones, entre números primos por la línea de disección media, observada en la gráfica:

En fórmula:

(g. 3) k /ln_k =  Cp = C_cp

Se lee:

Cp : Cantidad de números primos

Se lee:

C_cp : Cantidad de combinaciones primas

La Estructura NADIA de MJP esta conformada cualitativamente por celdas de igual tamaño, en donde se hallan binomios ordenados, éste binomio, depende de una suma en el cual se da un orden ascendente en cada fila, a medida que incrementa el valor del segundo término, mientras que el valor  del primer término permanece constante en cada fila, este incrementa en cada columna, mientras el segundo término permanece constante en cada columna.

Esta suma de binomios esta conformada por términos impares de valores consecutivos, tal que en las diagonales, mientras que a crece, b decrece, y a Λ b son mayores o igualo que 3, y como la primera tiene la misma cantidad de celdas que la prima fila a crece y b decrece si y solo si, a Λ b son mayores que 3. Además, si la primera fila tiene la misma cantidad de celdas que la primera columna, entonces, la estructura se define matemáticamente con la fórmula del factorial de 10; en ella se expresa la sumatoria de números enteros consecutivos, representando el incremento de la cantidad d celdas en la estructura, la fórmula es:

((a b)/ 2) V ((a + a ²)/ 2) V ((a( a + 1)/ 2)    

A esta fórmula se debe de reemplazarle los valores de a Λ b, debido a que el número seleccionado, y generalizado como k  (resultado del binomio) en la estructura, cumple con la regla propuesto por la conjetura de Goldbach, por lo cual, la cantidad de celdas que están dentro del valor k, depende de la fórmula:

[ ((k  -  3) - 1)/ 2 ]

Simplificando:  

[ (k  -  4) / 2 ]

Reemplazando:

En la fórmula  ((a(a + 1)/ 2), reemplazando nos queda:   

a = [ (k  -  4)/ 2 ]

b = [ [(k  - 4)/ 2 ]+ 1 ]

Por lo que:

((a (a + 1)/ 2) =  { [[[ (k  -  4)/ 2 ] [ [(k  - 4)/ 2 ]+ 1 ]/ 2] }

Ahora bien se sabe que k es un número par cualquiera, y se sabe también, que a través de la fórmula n/ln_n , obtenemos la cantidad de números primos que  existen hasta k, dentro de los grandes números, es decir, que si hasta k se hallaren n/ln_n  números primos, reemplazaré entonces n por k, debido a que k representa solo a los números pares, en fórmula,

nos queda:

k/ln_k  

Como he descartado las combinaciones entre números pares en la estructura, tengo en la primera columna al igual que en la primera fila k/ln_k  números primos, dentro de una cantidad de celdas, igual a [ (k  -  4)/ 2 ] por lo que gracias a la línea de disección media, la cual divide a la estructura en dos partes iguales, es por lo que puedo demostrar matemáticamente que las combinaciones entre números primos tienden al infinito y que además la cantidad de combinaciones entre números primos, es siempre mayor que la cantidad de celdas de la diagonal media, del cuadrado formado por las filas y columnas dentro de la estructura, cuadrado que tiene como punto de origen la línea de disección media, y que tiene como límite la razón [ (k  -  4)/ 2 ], a la vez la diagonal media del cuadrado contiene, todas las combinaciones posibles para formar un número k, menos las combinaciones inversas, que se hallan en la otra mitad de la diagonal, la fórmula general de este cuadrado, es la siguiente:

Téngase en cuenta, de tomarse como punto de origen la línea de disección media.

Si:

a = b

(g. 4) →[  [((((k  - 3) + 1)/ 2 ) + 1)/ 2 ]

Simplificando:

(g. 4 - 1) → [  [(((k  - 4)/ 2 ) + 1)/ 2 ]

En consecuencia:

a = b 

(g. 5) →  [(((k  - 4)/ 2 ) + 1)/ 2 ] ²

Así queda definido el cuadrado ya que [  [(((k  - 4)/ 2 ) + 1)/ 2 ]² es igual, a cualesquiera de sus lados.

En cambio si:

a ≠ b

(g. 6) →(g. 4) →[  (((((k  - 3) - 1)/ 2 )/2 )+ 1)/ 2 ]

Simplificando:

(g. 6 - 1) (g. 4) →[  [((k  - 6)  /2 ) + 1)/ 2 ]

En consecuencia:

a ≠ b

(g. 7) → [  [((k  - 6)  /2 ) + 1)/ 2 ] ²

El cuadrado queda ahora, así definido, debido a que, es igual a cualesquiera de sus lados. De esta manera es como obtengo dos cuadrado iguales, de dos maneras diferentes, es decir:

a = b Λ  a ≠ b

ya se ha visto que n/ln_n  es igual a la cantidad de primos en n, entonces para conocer la cantidad de números primos que se hallan en cada cuadrado, he de valerme de las variables a = b y  a ≠ b, teniendo en cuenta que la cantidad de números primos que existen en a, es siempre mayor que en b en los grandes números dentro de los cuadrados, debido a la línea de disección media, por lo que:

En a:

Si:

a = b

(g. 8)  (1/2k)/ k/ln_k  = C_{p (a)}

Se lee:

C_{p (a)}: cantidad de números  primos en a.

Si:

a ≠ b

(g. 9)  ((1/2k) - 1)/ k/ln_k  = C_{p (a)1}

Se lee:

C_{p (a)1} : cantidad de números primos en a₁

En b:

Si:

b = a

(g. 10) (k/ ln_k ) – (1/ 2k)/ ln_{(1/ 2 k)} = C_{p (b)}

Se lee:

C_{p (b)} : cantidad de números primos en b.

Si:

a ≠ b

(g. 11)  [(k/ ln_k ) -  [((1/ 2k ) – 1)/ ln_{((1/ 2k) – 1)} )]] = C_{p (b)1}

Se lee:

C_{p (b)1}: cantidad de números primos en b₁

Una vez conocida la cantidad de celdas en el cuadrado, se conoce por ende, la cantidad de combinaciones que existen dentro del mismo, entre números impares, entre números primos, y entre números impares y números primos, la solución es simple, para conocer la cantidades de combinaciones posibles, basta con conocer la cantidad de celdas que existe en uno de sus lados y multiplicarlo por si mismo, es decir, elevarlo al cuadrado como se visto anteriormente se deduce entonces, que al multiplicar la cantidad de números primos que existen en a, por la cantidad de números primos que existen en b, obtengo entonces, la cantidad de combinaciones entre números primos. Para conocer entonces las combinaciones entre números no primos; y las combinaciones entre números primos y números no primos, basta con restarle a la totalidad de combinaciones, las combinaciones primas.

Es decir:

La cantidad total de combinaciones primas en el cuadrado, es igual entonces, a:

si:

a = b 

(g. 12) → (C_{p ( a)})  (C_{p ( b)})       

Si:

a ≠ b

(g. 13) → (C_{p ( a) 1}) (C_{p ( b) 1})

De manera tal que la cantidad de combinaciones no primas, es igual a:

Si:

a = b

(g. 14) → { [ [(((k  - 4)/ 2 ) + 1)/ 2 ]²] – [(C_{p ( a)} ) * (C_{p ( b)} )] }

Si:

a ≠ b

(g. 15) → { [ [(((k  - 6)/ 2 ) + 1)/ 2 ]²]- [(C_{p ( a) 1}) (C_{p ( b) 1})] }

Es así, como hasta aquí he demostrado matemáticamente, que la cantidad de combinaciones primas en el cuadrado, es mayor que la cantidad de celadas que existen en el cuadrado, es mayor que la cantidad de celdas que existen en [  [(((k  - 4)/ 2 ) + 1)/ 2 ], o bien, en [  [(((k  - 6)/ 2 ) + 1)/ 2 ] por que, bastaría ahora demostrar si existe al menos, una combinación dentro de las diagonales medias de k, de cada cuadrado, es decir, que en la diagonal media de k, solo existe una diagonal media para cada k, y en general existe una diagonal existe una diagonal para cada celda de k.

Ahora bien, para demostrar que existe al menos una combinación prima dentro de cada diagonal media, utilizaré la misma estructura, pero con superposiciones o posiciones superpuestas, estas superposiciones, se deben a que la superposiciones, nacen en a + b = 6, (este primer binomio es la primera base de toda la estructura), / a Λ b = 3, hasta valor de k, para ello debemos de conocer previamente, cuantas combinaciones existen en la primera columna hasta k, es decir, [ (k  - 4)/ 2 ] después calcularemos lo siguiente:

Si:

a = b

Tomando como punto de origen a + b = 6 / a Λ b = 3

(G. 16) → [ [(((1/ 2k)+ 3 ) - 3) – 1) / 2 ]  

Simplificando nos queda:

(g. 17) [[((1/ 2k ) - 1)/ 2]

Y como:

a = b

Nos queda:

(g. 18) [[((1/ 2k) - 1)/ 2 ]²

Si:

a ≠ b Λ a < b tomando como punto de origen a +b = 6;/ a Λ b = 3

(g. 19) La primera fila contiene, [[((( 1/ 2 (k  - 2)) - 1)/ 2) + 1 ] combinaciones.

(g. 20) La primera columna contiene, [((1/ 2 (k  - 2)) - 1)/ 2 ] combinaciones.

Por lo que se obtiene la siguiente fórmula:

(g. 21) [ [((1/ 2(k - 2)) - 1)/ 2) + 1 ] [  [((1/ 2 (k  - 2))/ - 1)/ 2 ]]

Estas serán las bases de las superposiciones, dependiendo siempre de las variantes, si a = b, o si, a ≠ b, y desde allí en más, desarrollaré la estructura superponiéndole a la base:

Si:

A = b

(g. 22) [  [(1/ 2k) -1)/ 2 ]² + [  [((1/ 2k)  - 1)/ 2 ) + 1] * [ [((1/ 2k) – 1)/ 2) – 1] +  [((((1/ 2k) - 1)/ 2 ) + 1) + 1] * [((((1/ 2k) - 1)/ 2 ) - 1) - 1] +…+ [(((1/ 2k) - 1)/ 2 ) + 1n] * [(((1/ 2) - 1)/ 2 ) – 1n] = C_{csb (a, b)}

Se lee:

C_{csb (a, b)} : Cantidad de combinaciones en serie de base (a, b)

Si:

a ≠ b

(g. 23) [ [(((1/ 2(k - 2))  - 1)/ 2 ) + 1] * [ ((1/ 2(k - 2)) - 1)/ 2] ] + [[(((1/ 2 (k – 2 )) – 1)/ 2) + 1) + 1] * [ [(((1/ 2 (k - 2))  - 1)/ 2 ) - 1]] + [[(((((1/ 2 (k – 2 )) – 1)/ 2) + 1) + 1) + 1] * [ [(((1/ 2 (k - 2))  - 1)/ 2 ) – 1) – 1)]] +...+[  [((((1/ 2 (k - 2))  - 1)/ 2 ) + 1) + 1n]] * [  [(((1/ 2 (k - 2))  - 1)/ 2 ) – 1n]] = C_{csb (a 1, b 1)}

Se lee:

C_{csb (a1, b1)} : Cantidad de combinaciones en serie de base (a, b)

Para hallar la cantidad de combinaciones primas en estas estructuras de superposiciones, primero debo de conocer el valor de a Λ b, en [  [(1/ 2k)  - 1)/ 2 ], si a = b, y también el valor de a Λ  b, si a ≠ b en [  [((1/ 2k)  - 1)/ 2 ], por lo que calcularé ahora la cantidad de números primos combinados en las superposiciones, para ellos, utilizaré la fórmula n/ ln_n , reemplazando n, por el valor correspondiente en la estructura:

Es decir:

Si:

a = b

entonces:

n = 1/ 2k

/ n/ ln_n = 1/ 2k/ ln_{(1/ 2 k)} )= C_{p (a)} )

Se lee: cantidad de números primos en (a);

o en a Λ b;/ a = b      

Si:

a = b

entonces:

(g. 24)  C_{p ( a)}  * C_{p ( b)} = (C_{p ( a, b)}) ²

Se lee:

(C_{p ( a, b)}) ²: combinaciones primas en el cuadrado con (a, b) ²    

Si:

a ≠ b

n = ((1/ 2k) – 1) 

entonces:

(g. 25) n/ ln_n = ((1/ 2k) – 1)/ n/ ln_{n((1/ 2) – 1)} = C_{p  (a) 1}

Se lee:

C_{p ( a) 1} : Cantidad de números primos con   (a) ₁

→ n = ((1/ 2k) – 1) 

entonces:

(g. 26) n/ ln_n= ((1/ 2k) + 1)/ n/ ln_{((1/ 2k) + 1)} = C_{p (b) 1}

Se lee:

C_{p ( b) 1}: Cantidad de números primos con (b) ₁

entonces:      

(g. 27) [(C_{p ( a) 1}) * (C_{p ( b) 1})] = (C_{p ( a)} = C_{p ( a1, b1)}

Se lee:

C_{p ( a1, b1)} : combinaciones primas con (a _1,  b ₁)

He de aquí que se deduce, la cantidad de combinaciones no primas.

Si:

a = b

(g. 28) → (((1/ 2k) – 1)/ 2) ² – (C_{p ( a, b)}) ² = C _{~ p ( a, b)}

Se lee:

C _{~ p ( a, b)}: Combinaciones no primas con (a, b)

Si:

a ≠ b

(g. 29) → [ [ [(((1/ 2(k - 2))  - 1)/ 2 ) + 1] * [ ((1/ 2(k - 2)) - 1)/ 2] ] - (C_{p ( a1, b1)})] = C_{~p ( a1, b1)}

Se lee:

C_{~p ( a1, b1)} : combinaciones no primas con (a _1,  b ₁)

Una vez conocidas las bases, o primera posiciones, con su variante a = b Λ a ≠ b puedo comenzar a superponer a la base o primera posición la, 2ª, 3ª,…,n  posiciones hasta llegar a k, para lo cual, utilizaré las siguientes series para generalizar:

Si:

a = b

La serie es, entonces:

(g. 30) [ [(((1/ 2k) – 1/ 2] ² + [ ((1/ 2k) - 1)/ 2) + 1] * [(((1/ 2k) – 1)/ 2) – 1] + [(((1/ 2k) – 1)/ 2 ) + 1) + 1] * [(((1/ 2k) – 1)/ 2 ) - 1 ) - 1] +...+[(((1/ 2k) – 1)/ 2 ) + 1n] * [(((1/ 2k) – 1)/ 2 ) – 1n] = C_{csb ( a, b)}

Se lee:

Cp ( a, b) : Cantidad de números primos en (a, b)

Si:

a ≠ b

(g. 31) [ [(((1/ 2(k - 2))  - 1)/ 2 ) + 1] * [ ((1/ 2(k - 2)) - 1)/ 2] ] +

[ [((((1/ 2(k - 2))  - 1)/ 2 ) + 1) +1] * [ (((1/ 2(k - 2)) - 1)/ 2) - 1] ] +

[ [(((((1/ 2(k - 2))  - 1)/ 2 ) + 1) +1) + 1] * [ ((((1/ 2(k - 2)) - 1)/ 2) – 1) - 1] ] +...+[ [((((1/ 2(k - 2))  - 1)/ 2 ) + 1) +1n] * [ (((1/ 2(k - 2)) - 1)/ 2) – 1n] ] = C_{csb ( a1, b1)}

Se lee:

C_{csb ( a1, b1)} : combinaciones primas con (a _1,  b ₁)

Proseguiré con el análisis de las estructura de superposiciones, en donde calcularé la cantidad de combinaciones primas y no primas, en la base y demás posiciones para lo cual utilizaré, las fórmulas C_{p ( a, b)} para la cuadrada, tal que a = b,  para la base  a ≠ b, C_{p ( a1, b1)}  y para las demás posiciones hasta llegar al valor de k, la fórmula general de las combinaciones primas, de las demás superposiciones son:

Nos queda:

Si:

a = b

(g. 32) n/ ln_n = C_{p ( a, b)}    

Se lee:

C_{p ( a, b)}  : Cantidad de números primos en (a, b)

(g. 33) → [(1/ 2k/ ln_{(1/ 2 k)} ) * (1/ 2k/ ln_{(1/ 2 k)} )] = [(1/ 2k/ ln_{(1/ 2 k)} )] ² = (C_{p ( a1, b1)}  )²

Se lee:

(C_{p ( a1, b1)} ) ²: combinaciones primas con (a, b) 

Para:

a ≠ b

Se deduce que:

(g. 34) (1/ 2(k – 2)/ ln _{(1/ 2 (k - 2)} )  = C_{p ( a1)}

Se lee:

C_{p ( a1)} : cantidad de números primos con (a₁)                           

En cambio:

(g. 35) (1/ 2(k + 2)/ ln _{(1/ 2 (k + 2)} )  = C_{p ( b1)}

Se lee:

C_{p ( b1)} →: cantidad de números primos con (b₁)

(g. 36) (1/ 2(k – 2)/ ln _{(1/ 2 (k - 2)} ) * (1/ 2(k + 2)/ ln _{(1/ 2 (k + 2)} ) = (C_{p ( a1, b1)} )

Se lee:

(C_{p ( a1, b1)}): combinaciones primas con (a_1, b₁)

Se entiende que la cantidad de números primos para la 1ª, 2ª, 3ª…n, posiciones de la estructura de superposiciones la cantidad de números primos, es igual a:

Si:

a = b

(g. 37) (1/ 2k/ ln_{(1/ 2 k)} ) ² + [(1/ 2 (k + 2) / ln_{(1/ 2 (k + 2))} ) * (1/ 2 (k - 2) / ln_{(1/ 2 (k - 2))})] + [(1/ 2 (k + 4) / ln_{(1/ 2 (k + 4))} ) * (1/ 2 (k - 4) / ln_{(1/ 2 (k - 4))})] +…+ [(1/ 2 (k + 2n) / ln_{(1/ 2 (k + 2n))} ) * (1/ 2 (k – 2n₁) / ln_{(1/ 2 (k – 2n1))})] = C_{spb ( a, b)} 

Se lee:

C_{spb ( a, b)} : combinaciones en serie de números primos de base (a, b)

Téngase en cuenta, que estas fórmulas derivan de aproximaciones de la serie logarítmica (expuesta arriba), ya que las cantidades de combinaciones primas se obtienen, a través de las series son válidas, solo para los grandes números, pero indistintamente la serie mantiene la igualdad, ya que la misma resulta ser válida solo para los grandes números, las fórmulas a tener en cuenta, son las siguientes:

/ ((1/ 2(k + 2n) = k – 3

→ ((1/ 2(k – 2n)) = 3  

Por lo que:

((3 + (k – 3)) = k    

En consecuencia:

Si:

a ≠ b

(g. 38) (1/ 2 (k + 2) / ln_{(1/ 2 (k + 2))} ) * (1/ 2 (k - 2) / ln_{(1/ 2 (k - 2))})] + [(1/ 2 (k + 4) / ln_{(1/ 2 (k + 4))} ) * (1/ 2 (k - 4) / ln_{(1/ 2 (k - 4))})] + [(1/ 2 (k + 6) / ln_{(1/ 2 (k + 6))} ) * (1/ 2 (k - 6) / ln_{(1/ 2 (k - 6))})] +…+ [(1/ 2 (k + 2n₁) / ln_{(1/ 2 (k + 2n1))} ) * (1/ 2 (k – 2n₁) / ln_{(1/ 2 (k – 2n1))})] = C_{spb ( a1, b1)} 

Se lee:

C_{spb ( a1, b1)}  : combinaciones en serie de números primos de base (a_1, b₁)   

Téngase en cuenta que como ya he dicho anteriormente, derivan de aproximaciones de la serie logarítmica (expuesta arriba), ya que las cantidades de combinaciones primas se obtienen, a través de la serie válidas, solo para los grandes números, pero indistintamente, la serie mantiene la igualdad, ya que la misma resulta ser válida para los grandes números, las fórmulas a tener en cuenta, son las siguientes:

/ ((1/ 2(k + 2n ₁)) = k – 3

→ ((1/ 2(k – 2n₁)) = 3 

En consecuencia:

((3 + (k – 3)) = k    

Entonces, una vez calculada la cantidad de combinaciones entre números primos, hasta cada posición de la línea de disección media, a de restársele a la totalidad de combinaciones, es decir, a la estructura de superposiciones la cantidad de combinaciones entre números primos, para determinar cuantas combinaciones, entre números no primos existen.

Utilizando las generalizaciones nos queda:

Si:

a = b

(g. 39) → [(C_{csb ( a, b)}) - (C_{spb ( a, b)})] = (C_{s ~ p ( a, b)})

Se lee:

(C_{s ~ p ( a, b)}): combinaciones en serie no primas (a, b)

Si:

a ≠ b

(g. 40) → [(C_{csb ( a1, b1)}  ) - (C_{spb ( a1, b1)}  )] = (C_{s ~ p ( a1, b1)} )

Se lee:

(C_{s ~ p ( a1, b1)} ): combinaciones en serie no primas (a _1,  b ₁)  

Hemos visto así, como funciona la estructura de superposiciones, de ahora en más veremos, como funciona el mecanismo de la resolución de la estructura que depende de, si a = b, V si a ≠ b, pues de aquí depende su base, bastaría entonces con hallar la diferencia, de una serie con valor k, en general respecto a su consecutiva serie con valor k + 2, en la cantidad de combinaciones primas, tal que exista la menos una combinación prima en la serie de k, que se diferencie de la serie de k + 2, por lo que al demostrar que exista al menos una combinación prima, en cada una de las diagonales, quedaría demostrada la veracidad de la conjetura de Goldbach, de no ser así, quedaría demostrada la falsedad de tal enunciado. Pues hasta aquí, he llegado al límite de generalizaciones, que atentan contra el cierre de una demostración rotunda y determinante, que de fin al enunciado en su veracidad o falsedad, sin embargo estas generalizaciones son de gran importancia, y de gran valor logístico para demostrar a través del análisis matemático, que la conjetura de Goldbach, como dije anteriormente es verdadera, y que converge en fórmulas en una demostración existencial, es decir, que existe al menos una combinación prima, por cada número par del conjunto de números pares.

Anteriormente he analizado las estructuras que llevan por nombre, estructura NADIA de MJP, y la otra que he denominado, como estructura de superposiciones. En la primera estructura se observa que los números primos se extienden hacia el infinito, es decir, que la cantidad de números primos son infinitos (dato ya conocido), además se puede observar, que cada número primo se proyecta en la estructura de combinaciones binómicas, extendiéndose infinitamente, también puedo conocer cuantos números primos, y números no primos existen hasta k (datos ya conocido), se deduce a partir de este dato cuantas combinaciones primas y no primas existen, en [(k – 4)/ 2] ² , a la vez puedo conocer, cuantas combinaciones primas y combinaciones no primas existen hasta k, tomando como punto de origen la línea de disección media y se observa que cada diagonal esta conformada por celdas, que contienen binomios de igual valor para cada valor de k, en la segunda estructura se observa que las superposiciones da como resultado la diagonal, y a través de ella se puede determinar cuantas combinaciones primas y no primas existen en [(a ( a + 1))/ 2], pero esta generalización nos sigue llevando a un supuesto, y

 no a una generalización directa, que de respuesta al enunciado, de si es verdadero o falso, es por ello que valiéndome de todos los datos obtenidos y conociendo dentro de estos datos que para llegar a una solución, debía de hallar al menos una combinación prima en cada diagonal, es así como llegue a la conclusión, de que si en la fórmula , n/ ln_n la diferencia entre se obtenía un n + 2/ ln _{(n+ 2)} y n₁/ (ln_n1)se obtenía un incremento de la mantisa, hasta que incrementaba la característica de las parte de un logaritmo neperiano entonces, también debía de existir una diferencia entre:                 

(g. 41) ((k + 2)/ (ln _{(k+ 2)}) – (k/ ln _k))

cuyo incremento de la mantisa es parte diferencial del incremento de la característica, he de aquí, que se deduce que, la suma de las diagonales en su diferencia, es igual al incremento de la característica; pues se razona que si damos valor, 1 a la diferencia , y lo multiplicamos por (k – 4)/ 2 obtenemos la cantidad total de celdas de en combinación binómica por cada diagonal; pero se deduce que esta diferencia es menor que 1, debido a que como he dicho anteriormente, la diferencia de la mantisa por cada diagonal es parte diferencial del incremento de la característica, aprovecharé entonces esta diferencia, para llegar a la solución de la conjetura, en la cual, aparecen distintas fórmulas generales para las distintas combinaciones, es decir, para obtener la combinación entre primos, combinación entre no primos, y combinaciones entre números primos y números no primos.

Se entiende por lo expuesto anteriormente que la diferencia de la mantisa, se proyecta a través de toda la extensión de la diagonal media, por lo que en fórmula nos queda, la fórmula que ya se ha visto anteriormente:
Es decir:

((k + 2)/ (ln _{(k+ 2)}) – (k/ ln _k))

En donde se deduce que la cantidad de combinaciones entre números primos, es igual a la diferencia de la mantisa multiplicada por la característica de:

Si:

a = b

(g. 42) [(k/ ln _k) - ((1/ 2k) + 2)/ (ln _{((1/ 2k + 1)}))] = (C_{p ( k – ((1/ 2k) + 1 )})

Se lee:

(C_{p ( k – ((1/ 2k) + 1 )}): Cantidad de números primos en (C_{p ( k – ((1/ 2k) + 1 )})

a ≠ b

(g. 43) [(1/ 2k ₁/ ln _{(1/ 2k 1)}) - ((1/ 2k ₁)/ (ln _{((1/ 2k 1)}))] = (C_{p ( k 1– ((1/ 2k 1))})   

Se lee:

(C_{p ( k 1– ((1/ 2k 1))}): Cantidad de números primos en (C_{p ( k 1– ((1/ 2k 1))})  

K > k ₁  

(g. 44) (C_{p ( k – ((1/ 2k) + 1 )}) - (C_{p ( k 1– ((1/ 2k 1))}) = dif. _{m (a, b)}

Se lee:

dif. _{m (a, b)} : diferencia de la mantisa con (a, b)

Si:

K₁ > k

(g. 45) [(C_{p ( k1 – ((1/ 2k) + 1 )}) - (C_{p ( k – ((1/ 2k) + 1 ))})] = dif. _{m (a1, b1)}

Se lee:

dif. _{m (a1, b1)} : diferencia de la mantisa con (a ₁, b ₁)

Si:

a = b

(g. 46) [((1/ 2k) + 1)/ n/ ln_{((1/ 2k) + 1)}) – m] = car _{(a, b)}

Se lee:

car _{(a, b)}: característica con (a, b)

car _{(a, b)} = (C_{s ~ p ( a, b)})

Si:

a ≠ b

(g. 47) [((1/ 2k ₁)/ (ln _{((1/ 2k 1)})) – m₁] = car. _{(a1, b1)}

Se lee:

car. _{(a1, b1)}: característica con (a ₁, b ₁)

En consecuencia:

Si:

a = b

(g. 48) [( car. _{(a, b)}) (dif. _{m (a, b)})] = (C_{p ( diag. med.), (a, b)})

Se lee:

(C_{p ( diag. med.), (a, b)}): combinaciones primas en la diagonal media con (a, b)

Si:

a ≠ b

(g. 49) [(car. _{(a1, b1)} ) ( dif. _{m (a1, b1)} )] =(C_{p ( diag. med.), (a1, b1)})

Se lee:

(C_{p ( diag. med.), (a1, b1)}): combinaciones prima en la diagonal media con (a₁, b₁)

Pues se razona que, si la cantidad de combinaciones entre números primos. Las he calculado hasta la línea de disección media, por la diagonal media, entonces existe el duplo de combinaciones calculadas.

Es decir:

Si:

a = b

(g. 50)  [[( car. _{(a, b)}) (dif. _{m (a, b)})] 2] = (T_{c p ( diag. med.), (a, b)})

Se lee:

(T_{c p ( diag. med.), (a, b)}): total de combinaciones primas en el duplo de la diagonal media con (a, b)

Si:

a ≠ b

(g. 51) [[(car. _{(a1, b1)} ) ( dif. _{m (a1, b1)} )] 2] = (T _{c p ( diag. med.), (a1, b1)})

Se lee:

(T _{c p ( diag. med.), (a1, b1)}): Total de combinaciones primas en el duplo de la diagonal media con (a₁, b₁)

A sabiendas de que si k/ ln _k nos da la cantidad de números primos en k, entonces:

Si:

a = b

(g. 52) ((k/ ln _k) - (T_{c p ( diag. med.), (a, b)})) = (C_{p Λ ~ p (a, b)})

Se lee:

(C_{p Λ ∼ p (a, b)}): Cantidad de números primos y números no primos en (a, b)

Si:

a ≠ b

(g. 53) ((k/ ln _k1) - (T_{c p ( diag. med.), (a1, b1)})) = (C_{p Λ ~ p (a1, b1)})

(C_{p Λ ~ p (a1, b1)}): Cantidad de números primos y números no primos con (a₁, b₁)

La cantidad de combinaciones de los números no primos combinados entre si, es decir entre ~ p y  ~ p es (C _{p ~ Λ~ p})

Igual a :

(g. 54) [[((k - 4)/ 2 ] – (k/ ln_k)] = (C _{p ~ Λ ~ p})

Se deduce a partir de lo expuesto hasta aquí, que la diferencia que se proyecta por la diagonal es sumatoria de la mantisa, en el incremento de la característica de todo el conjunto de combinaciones, entre números primos de [(k - 4)/ 2], es decir, la suma de las diagonales contiene a la sección cuadrática, como ya se ha visto en las fórmulas anteriores, que nos retrotraen a las gráficas Nº 5 y Nº 6, pertenecientes a la estructura NADIA de MJP, y a la vez esta contiene todas las combinaciones primas hasta k, teniendo en cuenta la línea de disección media.

Téngase en cuenta que todas las igualdades en lo referente a los resultados de la Resolución de la Conjetura de Goldbach se podrían tomar como aproximaciones debido a que el valor de la mantisa es inconmensurable. Se dice entonces que los cálculos son aproximados, ya que he trabajado con ln.

Además se puede razonar que la diferencia de la mantisa entre k  y (k +2), es siempre menor que 1, independientemente de que los números primos, sean números primos gemelos, en las fórmulas implicadas en la Resolución de la conjetura de Goldbach según MJP.

Debemos también de tener en cuenta, que esta fórmulas son aplicables, tanto para los números positivos como para los números negativos, es decir que puede añadírsele el símbolo (±) a cada una de las fórmulas contenidas dentro de la extensión de este análisis matemático, se entiende entonces, que todas las estructuras tienen un sentido opuesto, dada por el conjunto de números negativos, las cuales denominaré como anti estructuras, es decir; añadiré el prefijo Anti a todas las estructuras, que se hallan dentro de este estudio.

A continuación, se verá, que la estructura formada entre binomios de números pares e impares, cuyo resultado es evidentemente impar, la expondré solo para demostrar cual es su conformación en cuanto a su análisis matemático, debido a que no es de utlidad para resolución de la conjetura propuesta por Christian Goldbach, como ya lo he enunciado al comienzo de este trabajo.

La estructura es la siguiente y la misma lleva por nombre: Estructura de Posiciones con Uniones de Pares he Impares de MJP, o bien para abreviar, estructura PUPI, de MJP. (Ver en el anexo, gráfica (f)).

La cantidad de celdas que contienen binomios en la primera fila, como en la primera columna de la estructura, esta determinada, por el resultado del binomio elegido, que será un impar Imp., cualesquiera, tal que en el binomio:

a ≥ 3  Λ b  ≥ 4  en consecuencia(a + b) ≥ 7

Para Imp., nos queda:

[(Imp – 3) – 3) + 1)/ 2 ] = (C_{b ( a, b)})

Simplificando:

[(Imp – 5)/ 2 ] = (C_{b ( a, b)})

Se lee:

(C_{b ( a, b)}): cantidad de binomios con (a, b)

Se observa en la estructura, que la línea de disección media, separa a la cantidad total de combinaciones, en dos partes iguales, y a la vez esta mitad crece según la fórmula del factorial de 10, que ya la he expuesto al principio. Se deduce entonces que el duplo de esta mitad, es la cantidad de combinaciones buscada.

Es decir:

Ʃ = [(a (a + 1)/ 2]

→ a = [(Imp – 5)/ 2 ]

/ a + 1 = [[(Imp. – 5)/ 2 ] + 1]

En consecuencia:

Ʃ = [(a (a + 1)/ 2] = [[((Imp – 5)/ 2) (((Imp – 5)/ 2) + 1)]/ 2 ]

Tal que:

Ʃ = [[[((Imp – 5)/ 2) (((Imp – 5)/ 2) + 1)]/ 2 ]  2] = (C_{t c ( a, b)})

Se lee:

(C_{t c ( a, b)}) : Cantidad total de combinaciones con (a, b)

Entonces si (C_{t c ( a, b)}) es igual, al total de combinaciones con (a, b), se deduce que la cantidad de celdas que no tienen binomios, (las cuales he denominado como: celdas vacías), hasta un Imp., cualesquiera, esta determinada por la cantidad de celdas en la estructura, es decir las celdas vacías y las que contienen binomios (dato ya conocido), se deduce a partir de este dato, que la cantidad  de celdas en las filas es igual, que la cantidad total de celdas que no contienen las columnas, tal que:

Si:

[(Imp. – 5)/ 2 ]  = (C_{t  celd. ( a, b)})

Se lee:

(C_{t  celd. ( a, b)}): Cantidad de celadas con (a, b)

En consecuencia si la cantidad de celadas en las filas, es igual a la cantidad de celdas en las columnas, se deduce entonces que la cantidad total de celdas, deriva de la fórmula del factorial de 10.

Es decir, si:

Ʃ = [(a (a + 1)/ 2]

→ a = (Imp – 5)

/ a + 1 = [(Imp. – 5) + 1]

En consecuencia:

Ʃ = [(a (a + 1)/ 2]

→ [(Imp – 5) ((Imp – 5) + 1)]/ 2 ] = (C_{t c ( a1, b1)})

Se lee:

(C_{t c ( a1, b1)}): Cantidad total de combinaciones con (a₁, b₁) ;( en filas y columnas)

Pues una vez conocida esta cantidad de combinaciones le restaremos a esta entonces, la cantidad total de combinaciones con (a, b).

Por lo que:

Ʃ =[[[(Imp – 5) ((Imp – 5) - 1)] -  [(Imp – 5) ((Imp – 5) + 1)]/ 2 ]] 2 ] = (C_{t celd. v ( a1, b1)}): Cantidad total de celdas vacías con (a, b)

Así, queda definida la estructura PUPI de MJP, igualmente podría definir la estructura entre suma de pares, tal que a Λ b, sean números pares que formen un binomio con resultado evidentemente par, pero esto de hecho sería en vano, ya que esto no es lo que nos solicita la conjetura de Goldbach.

Así es como he llegado al final de esta resolución, que le he dado por nombre:

Resolución de la Conjetura de Goldbach Según MJP